RNN部分问题的原理解释

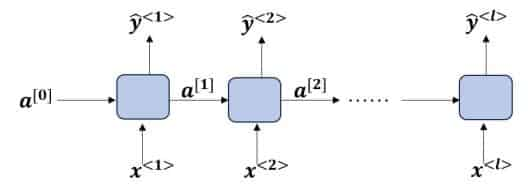
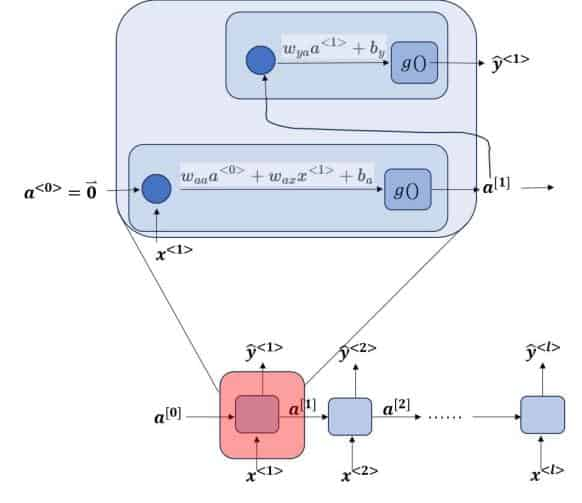
1. RNN的前向传播原理

以一个Many-to-Many的简单RNN为例(输入输出维度相等)：

每一时间单位的前向计算过程为：

$$\begin{aligned} & a^{<t>} = f(w_{aa}a^{<t-1>} + w_{ax}x^{<t>} + b_a) \\ & z^{<t>} = w_{ya}a^{<t>} + b_y\\ & \hat{y}^{<t>} = g(z^{<t>}) \end{aligned}$$

第一步也可以简写为：

$$a^{<t>} = f(w_{a}[a^{<t-1>},x^{<t>}]^T + b_a)$$

$w_{ya}$也记作$w_y$.

有的RNN论文中还会把第一步的激活函数放到里面，即写作：

$$a^{<t>} = w_{aa}f(a^{<t-1>}) + w_{ax}x^{<t>} + b_a$$

这两个公式在宏观意义上被认为是等价的。

2. RNN的损失函数与反向传播(Back Propagation Through Time, BPTT)

现在，通过上一步已经能够找到预测值$\hat{y}^{<t>}$，在真实值$y^{<t>}$已知的条件下，单步的损失可以借助交叉熵定义为：(当然也可以用残差定义)

$$\mathcal{L}^{<t>}(\hat{y}^{<t>}, y^{<t>}) = -y^{<t>}\log\hat{y}^{<t>} - (1-y^{<t>})\log(1-\hat{y}^{<t>})$$

模型总的损失函数为：(取时间平均，某些论文也没有做时间平均，个人感觉时间平均没有太大的必要)

$$L(\hat{y}, y) = \frac{1}{T} \sum_{t=1}^{T_y} \mathcal{L}^{<t>}(\hat{y}^{<t>}, y^{<t>})$$

优化目标为：

$$J = \argmin_{w_a,w_y,b_a,b_y}{L(\hat{y}, y})$$

分析可知，优化的目标函数与四个参量有关：$w_a,w_y,b_a,b_y$。因此，计算损失函数相对于这四者的偏导数，不断进行参数更新，直到模型收敛，就是求解BRTT的大致过程。

为便于分析，不考虑偏置项对模型收敛的影响，只考虑权重矩阵。首先分析$\frac{\partial L}{\partial w_y}$: $w_y$是一个与输出的预测值$\hat{y}^{<t>}$相关的值，因此根据链式法则有：

$$\frac{\partial L}{\partial w_y} = \frac{\partial L}{\partial g(z^{<t>})} \frac{\partial g(z^{<t>})}{\partial w_y}$$

分两项考虑，第一项：

$$\frac{\partial L}{\partial g(z^{<t>})} = \frac{1}{T}\sum_{t=1}^{T_y}\frac{\partial \mathcal{L}}{\partial g(z^{<t>})}$$

第二项：

$$\frac{\partial g(z^{<t>})}{\partial w_y} = \frac{\partial [g(w_{y}a^{<t>} + b_y)]}{\partial w_y}$$

其次分析$\frac{\partial L}{\partial w_{a}}$:

$$\begin{aligned} \frac{\partial L}{\partial w_a} &= \frac{1}{T}\sum_{t=1}^{T_y}\frac{\partial \mathcal{L}^{<t>}(\hat{y}^{<t>}, y^{<t>})}{\partial w_a} \\ &= \frac{1}{T}\sum_{t=1}^{T_y} \frac{\partial \mathcal{L}^{<t>}(\hat{y}^{<t>}, y^{<t>})}{\partial \hat{y}^{<t>}} \frac{\partial \hat{y}^{<t>}}{\partial a^{<t>}} \frac{\partial a^{<t>}}{w_a} \\ &= \frac{1}{T}\sum_{t=1}^{T_y} \frac{\partial \mathcal{L}^{<t>}(\hat{y}^{<t>}, y^{<t>})}{\partial g(w_{y}a^{<t>} + b_y)} \frac{\partial g(w_{y}a^{<t>} + b_y)}{\partial a^{<t>}}\frac{\partial a^{<t>}}{w_a} \end{aligned}$$

在上式中，第一项和第二项不需要循环计算，而第三项是需要不断地计算每一步参数$w_a$对$a^{<t>}$的影响。

$$\frac{\partial a^{<t>}}{w_a} = \frac{\partial f(w_{a}[a^{<t-1>},x^{<t>}]^T + b_a)}{\partial w_a} + \frac{\partial f(w_{a}[a^{<t-1>},x^{<t>}]^T + b_a)}{\partial a^{<t-1>}}\frac{\partial a^{<t-1>}}{\partial w_a}$$

观察上面的递归式，不难发现有以下的结构规律，对于$a^{<0>} = 0$，设${a^{<i>}}$,${b^{<i>}},{c^{<i>}}$为一个序列：

$$\begin{aligned} & a^{<1>} = b^{<1>} + c^{<1>}a^{<0>} = b^{<1>} \\ & a^{<2>} = b^{<2>} + c^{<2>} a^{<1>} = b^{<2>} + b^{<1>}c^{<2>} \\ & a^{<3>} = b^{<3>} + c^{<3>} a^{<2>} = b^{<3>}+b^{<2>}c^{<3>} + b^{<1>}c^{<2>}c^{<3>} \\ & \dots \\ & a^{<t>} = b^{<t>} + \sum^{t-1}_{i=1}(\prod \limits_{j=i+1}^t c^{<j>})b^{<i>} \end{aligned}$$

下面把${a^{<i>}}$,${b^{<i>}},{c^{<i>}}$分别替换成$\frac{\partial a^{<t>}}{w_a}$,$\frac{\partial f(w_{a}[a^{<t-1>},x^{<t>}]^T + b_a)}{\partial w_a}$,$\frac{\partial f(w_{a}[a^{<t-1>},x^{<t>}]^T + b_a)}{\partial a^{<t-1>}}$

最终算式为

$$\begin{aligned} a^{<t>} &= b^{<t>} + \sum^{t-1}_{i=1}(\prod \limits_{j=i+1}^t c^{<j>})b^{<i>} \\ \frac{\partial a^{<t>}}{\partial w_a}&=\frac{\partial f(w_{a}[a^{<t-1>},x^{<t>}]^T + b_a)}{\partial w_a} + \sum^{t-1}_{i=1}(\prod \limits_{j=i+1}^t \frac{\partial f(w_{a}[a^{<j-1>},x^{<j>}]^T + b_a)}{\partial a^{<j-1>}})\frac{\partial f(w_{a}[a^{<i-1>},x^{<i>}]^T + b_a)}{\partial w_a} \end{aligned}$$

3. RNN的时序记忆能力短的原因？

为便于分析，假设隐藏层的激活函数为线性激活函数（也可以说没有激活），将RNN的前馈输出展开：

$$\begin{aligned} a^{<t>} &= w_{aa}a^{<t-1>} + w_{ax}x^{<t>} + b_a \\ &= w_{aa}[(w_{aa}a^{<t-2>} + w_{ax}x^{<t-1>} + b_a)]+ w_{ax}x^{<t>} + b_a \\ &= w_{aa} \space w_{aa}a^{<t-2>} + w_{aa} \space w_{ax}x^{<t-1>} + w_{aa} \space b_a)]+ w_{ax}x^{<t>} + b_a \\ &= ... \end{aligned}$$

不难看出，每一次的前向传播都会对之前的激活值产生影响，一旦序列较长，模型对于附近的值的敏感程度就明显高于之前的输入，RNN表现出了“遗忘”的现象。

4. RNN的梯度爆炸与梯度消失成因？

假定我们使足够简单的线性激活函数作为隐藏层的激活函数$f()$,（或者说不适用任何激活函数） 根本原因在求解$\frac{\partial a^{<t>}}{\partial w_a}$时，出现了：

$$\begin{aligned} & (\prod \limits_{j=i+1}^t \frac{\partial f(w_{a}[a^{<j-1>},x^{<j>}]^T + b_a)}{\partial a^{<j-1>}}) \\ = &(\prod \limits_{j=i+1}^t \frac{\partial [w_{aa}a^{<j-1>} + w_{ax}x^{<j>} + b_a]}{\partial a^{<j-1>}})\\ = & (\bold {w_{aa}})^l \\ & where: \space l = t-j \end{aligned}$$

即$\frac{\partial a^{<t>}}{\partial a^{<j>}} = (\bold {w_{aa}})^l$

假定 $\bold w_{aa}$ 可对角化，令$\bold {w_{aa}}$的n个特征值为{$\lambda_1, \lambda_2, ... , \lambda_n\}$, 且满足$|\lambda_1| \geq |\lambda_2| \geq ... \geq |\lambda_n\|$。其对应的特征向量为$\bold q_1, \bold q_2, ... , \bold q_n$，他们组成向量基。则在这个向量空间下:

$$\frac{\partial \hat{y}^{<t>}}{\partial a^{<t>}} = \sum_{i=1}^{n}c_i \bold{q_i}^T$$

且有(待求证？)：

$$\bold q_i^T(\bold w_{aa}^T)^l = \lambda_i^l \bold q_i^T$$

如果有$j$满足 $c_j \neq 0, {\forall}j^{'} \lt j,c_j = 0$

$$\begin{aligned} \frac{\partial \hat{y}^{<t>}}{\partial a^{<t>}}\frac{\partial a^{<t>}}{\partial a^{<j>}} &= c_j \lambda_j^l \bold q_j^T + \lambda_j^l \sum_{i=j+1}^{n}c_i \frac{\lambda_i^l}{\lambda_j^l} \bold q_i^T \\ & \approx c_j \lambda_j^l \bold q_j^T \end{aligned}$$

因为$|\frac{\lambda_i}{\lambda_j}|<1,(i > j)$, $\lim_{l \to \infty}|\frac{\lambda_i}{\lambda_j}|^l = 0$. 由此我们可以看出，$\frac{\partial a^{<t>}}{\partial a^{<j>}}$随着$l$的增大而指数级增大，且是沿着$\bold q_j$的方向增长。

虽然上面的证明$\bold w_{aa}$可以对角化，但是如果用Jordan正则表达式，上面的证明可以扩展到不仅仅是最大特征值的特征向量，而且可以考虑共享相同最大特征值的特征向量所跨越的整个子空间，扩展到更广泛的情况。（这一步尚且还没有读懂 （恶补矩阵论去了） ）

于是我们能够得出梯度爆炸或梯度消失的充分条件：

梯度爆炸的充分条件：$t \to \infty $时，$\lambda_1$（$\bold{w_{aa}}$的所有特征值中最大的）$\gt 1$。

梯度消失的充分条件：$t \to \infty $时，$\lambda_1$（$\bold{w_{aa}}$的所有特征值中最大的）$\lt 1$。

以上讨论的都是基于激活函数是线性的（即没有使用任何激活函数）。如果是针对非线性函数，则有非线性函数的输出一定有界这一特性，即：

$$||diag(f(x^{<t>}))|| \leq \gamma (\gamma \in \real)$$

证明：只要$\lambda_1 \lt \frac{1}{\gamma}$, 其中$\lambda_1$是权重矩阵$w_{aa}$中的最大特征值，就足以发生梯度消失问题

$$\forall k, ||\frac{\partial a^{<k+1>}}{\partial a^{<k>}}||_2 \leq ||\bold w_{aa}^T||\space||diag(f'(x^{<k>}))|| \lt \frac{1}{\gamma}\gamma = 1$$

于是$\exist \eta \in \real$,满足$\forall k,||\frac{\partial a^{<k+1>}}{\partial a^{<k>}}||_2 \leq \eta \lt 1$

$$\frac{\partial \hat{y^{<t>}}}{\partial x^{<t>}} (\prod \limits_{i=k}^{t-1} \frac{\partial a^{<i+1>}}{\partial a^{<i>}}) \leq \eta^{t-k} \frac{\partial \hat{y^{<t>}}}{\partial a^{<t>}}$$

因为$\eta \lt 1$, 根据上式，模型非常深的时候（$t-k$很大），梯度指数下降至0值附近。

根据梯度消失的证明思路，我们也很容易得到梯度爆炸的条件：$\lambda_1 \lt \frac{1}{\gamma}$

从微分方程到RNN

令$\vec{s}(t)$是$d$-维状态，考虑一个一般的非线性一阶非均质常微分方程，描述状态信号随时间的变化。(这很像状态估计问题)

$$\frac{d\vec{s}(t)}{dt} = \vec{f}(t) + \vec{\phi}$$

状态随时间变化可以认为有两部分在作用，其中前者与输入$\vec{x}(t)$（或者引用状态估计问题中的说法：观测）有关:

$$\vec{f}(t) = \vec{h}(\vec{s}(t), \vec{x}(t))$$

于是，一个在物理、化学、工程领域非常常见的方程式就出现了：（至少原作者Sherstinsky是这么说的）

$$\frac{d\vec{s}(t)}{dt} = \vec{h}(\vec{s}(t), \vec{x}(t)) + \vec{\phi}$$

除此之外，$\vec{f}(t)$还有其他形式，比如脑动力学研究中的加性模型（Addictive Model）：

$$\vec{f}(t) = \vec{a}(t)+\vec{b}(t)+\vec{c}(t)$$

加性模型的三个时间向量如下定义：

$$\begin{aligned} {\vec{a}}(t)& =\sum_{k=0}^{K_{s}-1}\vec{a}_{k}(\vec{s}(t-\tau_{s}(k))) \\ {\vec{b}}(t)& =\sum_{k=0}^{K_{r}-1}\vec{b}_{k}(\vec{r}(t-\tau_{r}(k))) \\ \vec{r}(t-\tau_{r}(k))& =G\left(\vec{s}(t-\tau_{r}(k))\right) \\ \vec{c}(t)& =\sum_{k=0}^{K_{x}-1}\vec{c}_{k}(\vec{x}(t-\tau_{x}(k))) \end{aligned}$$

式中，$\vec{r}(t)$是状态$\vec{s}(t)$的变换，$G()$为非线性激活函数。状态随时间的变化就可以展开写成如下形式：

$$\begin{aligned} \frac{d\vec{s}(t)}{dt}& =\sum_{k=0}^{K_{s}-1}\vec{a}_{k}(\vec{s}(t-\tau_{s}(k)))+\sum_{k=0}^{K_{r}-1}\vec{b}_{k}(\vec{r}(t-\tau_{r}(k)))+\sum_{k=0}^{K_{x}-1}\vec{c}_{k}(\vec{x}(t-\tau_{x}(k)))+\vec{\phi} \\ \vec{r}(t-\tau_{r}(k))& =G\left(\vec{s}(t-\tau_{r}(k))\right) \end{aligned}$$

该方程是一个具有离散延迟的非线性常延迟微分方程 (DDE)。首项是

5. LSTM的前向传播

在LSTM（以及GRU）中，我们要引入一个新概念：候选记忆元（candidate memory cell）,用$c$表示，在每一个步长里，用候选值$\tilde{c}^{<t>}$重写之前记忆的值$c$。（这里的c和传统RNN中的隐藏层激活值a从本质上来说是同一个表达）。为了应对RNN的"遗忘问题"，LSTM采取的策略是（核心思想）建立一些门函数，其中一个门用来从单元中输出条目，我们将其称为输出门（output gate,$\Gamma_o$）。 另外一个门用来决定何时将数据读入单元，我们将其称为输入门/更新门（input/update gate,$\Gamma_u/\Gamma_i$）。 我们还需要一种机制来重置单元的内容，由遗忘门（forget gate, $\Gamma_f$ ） 来管理。

$$\begin{aligned} &\tilde{c}^{<t>} = \tanh(w_c[a^{<t-1>},x^{<t>}] + b_c) \\ &\Gamma_i = \sigma(w_i[a^{<t-1>},x^{<t>}] + b_u) \\ &\Gamma_f = \sigma(w_f[a^{<t-1>},x^{<t>}] + b_f) \\ &\Gamma_o = \sigma(w_o[a^{<t-1>},x^{<t>}] + b_o) \\ &c^{<t>} = \Gamma_i \times \tilde{c}^{<t>} + \Gamma_f \times c^{<t-1>} \\ &a^{<t>} = \Gamma_o \times \tanh(c^{<t>}) \end{aligned}$$

6. LSTM中的BPTT：

基于$a^{<t>}$, 可以得到每一步的预测值：

$$\hat{y}^{<t>} = g(w_ya^{<t>} + b_y)$$

单步损失$\mathcal{L}^{}(\hat{y}^{}, y^{}) $略去，（与上文的传统RNN一样），模型总损失为：

$$L(\hat{y}, y) = \frac{1}{T} \sum_{t=1}^{T_y} \mathcal{L}^{<t>}(\hat{y}^{<t>}, y^{<t>})$$

优化目标为：

$$J = \argmin_{w_c,w_f,w_i,w_o,w_y,b_c,b_f,b_i,b_o,b_y}{L(\hat{y}, y})$$

为了便于讨论，依然忽略偏置值对模型的影响，着重考虑权重矩阵。

首先是损失函数关于$\bold w_f$的导数

$$\begin{aligned} & \frac{\partial L}{\partial \bold w_f} = \sum_{i=1}^{t} \frac{\partial L^{<i>}}{\partial \bold w_f^{<i>}} \\ & \frac{\partial L^{<t>}}{\partial \bold w_f^{<t>}} = \frac{\partial L^{<t>}}{\partial y^{<t>}} \frac{\partial y^{<t>}}{\partial a^{<t>}} \frac{\partial a^{<t>}}{\partial c^{<t>}} \frac{\partial c^{<t>}}{\partial \Gamma_f^{<t>}} \frac{\partial \Gamma_f^{<t>}}{\partial \bold w_f^{<t>}} \\ \end{aligned}$$

公式之所以会分为五项，是因为在反向传播过程中存在两个“分岔路口”。，再往下求解之前一个时刻，则公式内部的$\frac{\partial a^{<t>}}{\partial c^{<t>}}$继续展开为五项。

求解$\bold w_i$的影响的思路和$\bold w_f$类似，同样存在五项；求解前一时刻的$\bold w_o,\bold w_c$的影响则会分别出现4条链路（4项）。对于$w_y$的影响的求解就较为简单，因为不需要之前时刻的信息。

LSTM的时序记忆能力强的原因？

LSTM的核心是前向传播中的记忆单元，通过模型学习，调节三个门函数的权重矩阵的值，有可能会产生$\frac{\partial c^{<t>}}{\partial c^{<t-1>}} \approx 1$,从而有

$$\prod \limits_{i=k}^{t}\frac{\partial c^{<i>}}{\partial c^{<i-1>}}\approx 1$$

因为有记忆单元的存在，LSTM能实现在较长的时间内“记住”之前的信息。

LSTM对BPTT的梯度爆炸和梯度消失的缓解

LSTM对梯度消失的缓解依然是在更新记忆单元。反向传播的过程中涉及计算$\frac{\partial c^{<t>}}{\partial c^{<t-1>}}$,将其展开能够得到：

$$\begin{gathered} \frac{\partial c^{<t>}}{\partial \Gamma_f^{<t>}}\frac{\partial \Gamma_f^{<t>}}{\partial a^{<t-1>}}\frac{\partial a^{<t-1>}}{\partial c^{<t-1>}}+\frac{\partial c^{<t>}}{\partial \Gamma_i^{<t>}}\frac{\partial \Gamma_i^{<t>}}{\partial a^{<t-1>}}\frac{\partial a^{<t-1>}}{\partial c^{<t-1>}} \\ +\frac{\partial c^{<t>}}{\partial \tilde{c}^{<t>}}\frac{\partial \tilde{c}^{<t>}}{\partial a^{<t-1>}}\frac{\partial a^{<t-1>}}{\partial c^{<t-1>}} + \frac{\partial c^{<t>}}{\partial c^{<t-1>}} \end{gathered}$$

$$\begin{gathered} &=c^{<t-1>}\sigma^{'}(w_{xf}x^{<t>} + w_{af}a^{<t-1>} + b_f) \Gamma_o tanh^{'}(C^{(k-1)}) \\ &+\tilde{c}^{<t>}\sigma^{'}(w_{xi}x^{<t>} + w_{ai}a^{<t-1>} + b_i)\Gamma_o tanh^{'}(C^{(k-1)}) \\ &+\Gamma_i^{<t>}tanh^{^{\prime}}(w_{ac}a^{<t-1>}+w_{xc}x^{<t>} + b_c)tanh^{^{\prime}}(C^{(k-1)}) \\ &+f^{(t)} \end{gathered}$$

$$\prod_{k=t+1}^T\frac{\partial c^{<k>}}{\partial c^{<k-1>}}=(f^{(k)}f^{(k+1)}\ldots f^{(T)})+other$$

在LSTM迭代过程中，针对 $\prod_{k=t+1}^T\frac{\partial c^{<k>}}{\partial c^{<k-1>}}$而言，模型在学习的过程中，有了三个门函数的权重矩阵，每一步可以通过更改权重矩阵去自主选择在[0,1]之间，或者大于1，整体$\prod_{k=t+1}^T\frac{\partial c^{<k>}}{\partial c^{<k-1>}}$也就不会一直减小，远距离梯度不至于完全消失，也就能够解决RNN中存在的梯度消失问题。

LSTM和ResNet中的残差逼近思想有些相似，通过构建从前一时刻记忆单元到下一时刻记忆单元的“短路连接”，使梯度得已有效地反向传播，以应对梯度消失。

至于梯度爆炸问题，LSTM的提出不能说完全规避，从RNN的单项式连乘到LSTM的多项式连乘，后者还有相加运算，有可能梯度值大于1。毕竟LSTM的提出主要是为了缓解梯度消失的问题。