Rethinking trending paradigms of neural networks
写在前面
近日博主发现2024、2025年,社区中涌现了一大批做Looping Network的工作(包括但不限于做数独、做迷宫、做路径规划。。。),一直想探索Looping在语言类任务的效果。最近又看到马里兰大学的研究,把Skipping和Looping结合到一起用MCST(蒙特卡洛搜索树)做最优的探索,居然在语言类的常规任务上取得了很好的提升(我之前自己做Looping在这些任务都是掉点的/可能是没做什么Continuous Training和别的)。于是想好好研究一下Looping背后的机制和原理,期望能带来某些insights。
现代神经网络的三种信息处理范式
| 形式化表述 | 举例 | 说明 |
|---|---|---|
| MLP, CNN, Decoder-only Transformer | 无状态(stateless)映射:一次性输入 → 输出 | |
| RNN | 有状态(stateful)动态系统:每步输入与历史状态共同决定输出与新状态 | |
| Deep Equilibrium Model (DEQ), Neural ODE, hierarchical reasoning model(HRM), tiny recursive model(TRM) | 分离状态更新与读出(state transition + readout):内部状态自演化,输出从状态读出 |
表格中被称为implicitly-defined layers (详见 NeurIPS 2024: Understanding Representation of Deep Equilibrium Models from Neural Collapse Perspective)。
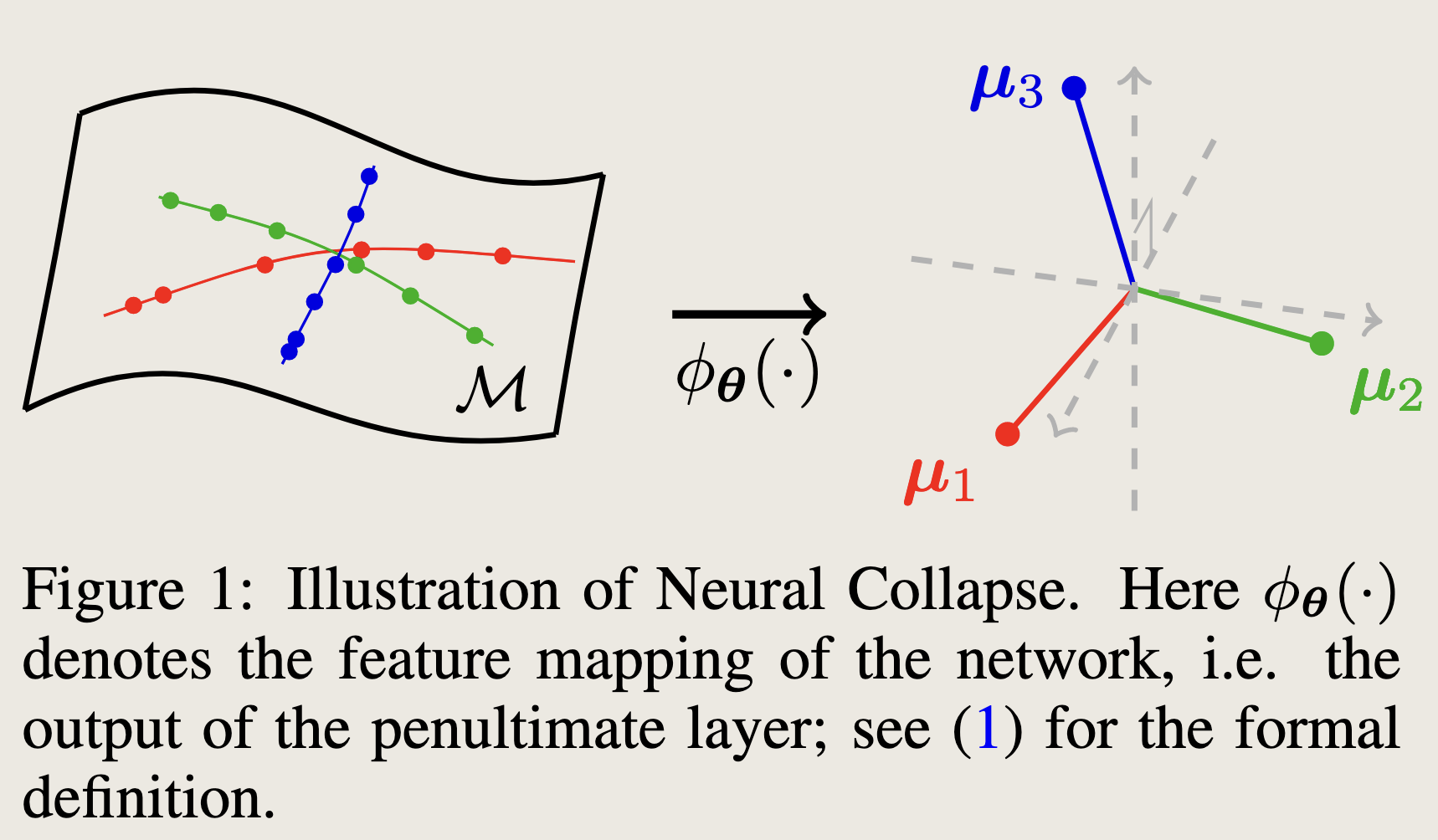
Neural Collapse (神经[网络表征]坍缩, )
当模型处于训练的最终阶段 (terminal phase of training, TPT),或更准确地说,达到零训练误差时,最后一层的特征的类内均值和分类头的向量收敛到平衡数据集上的单纯形等角紧框架 (Equiangular Tight Frame, ETF) 的顶点。
Simplex Equiangular Tight Frame: 一组处于某个n维空间的K个点的集合 被称为单纯形等角紧框架如果满足:
是单位矩阵,是纯1向量, 是部分正交矩阵,使得 .
的四个属性:
- 方差坍缩(Variance Collapse):类内特征(即最后一层的feature map)收敛为唯一向量,即对于同一个标签类中的任意样本,通过训练过程,其特征 满足。
- 收敛于单纯形等角紧框架(Convergence to Single ETF):每个类的最佳特征的平均值(即)折叠到单纯形 ETF 的顶点。
- 收敛于自对偶(Convergence to Self-duality):在训练收敛后,分类器学到的权重方向和数据特征本身的类别中心方向是一致的,即. (自对偶意味着:这两个原本不同视角的问题,在深度网络训练后会收敛到同一个解.)
- 最近邻原则(Nearest Neighbor):分类器根据特征向量和分类器权重之间的欧几里得距离来确定类别。
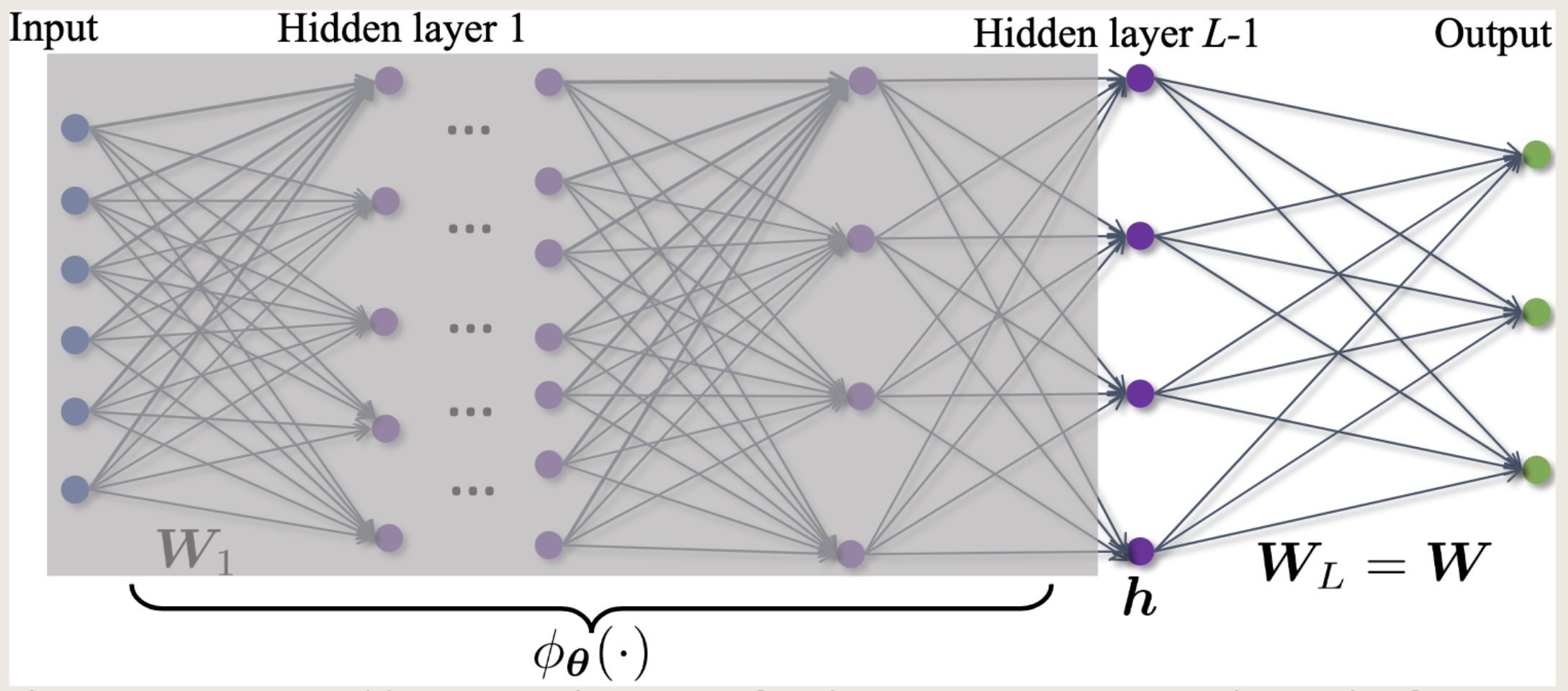
无约束特征模型(Unconstrained Feature Model, UFM)
也叫层剥离模型(Layer-peeled Model),指的是神经网络的最后一层特征与最后一层分类器一起的建模,被视为可以学习的优化变量。
在UFM的先验假设下,大多数研究都是基于1-2层常规权重,但是也有将其扩展到分析M层线性层的。
少数[特征表征]崩溃(Minority Collapse, MC)
在不平衡的类间样本中,通常不会发生。这种现象的出现是由于训练样本数量类间不平衡,导致在充分拟合某些类别的特征方面存在挑战。这通常被称为MC。这种现象是不好的,因为会影响神经网络本身的泛化性(本质是数据呈现长尾分布的问题)。有很多种方法来缓解MC,例如convex relaxation,修改loss,加正则,reweighting,AutoBalance,logit监督等等。
写到这里,我们需要澄清一下,我们针对神经表征坍缩的研究依然停留在分类问题,没有拓展到(至少我没有看到过)语言类的自回归输出、生成类任务等领域。
一个直观的想法是:既然是一个分类网络训练终点的重要标志,那为什么不用这些规律去做显式的监督,让网络更快地达到收敛效果。