写在前面

任课教师：许超，Bakhadyr Khoussainov
参考教材：MIT 6.042J 教材

知识点总结

好心的许老师在课程群里发了：submodular function, matroid, matroid intersection, base, graph coloring, independent set, clique, binary matrix multiplication, shortest path

alt text

。。。但真的难度很高（我都没听过啊啊啊啊）

1. 次模函数（Submodular Function）

Ref（漫长的4h雅思听力）：Submodularity and Optimization – Jeff Bilmes (Part 1)

1.1 次模、超模与模函数的基本定义

Def. 1.1.1(次模的定义)：Given a finite ground set(有限的基集合) $V$ , a function $f: 2^V \rightarrow \mathbb{R}$ is said to be submodular if

$f(A)+f(B)\ge f(A\cup B)+f(A\cap B),\quad \forall, A,B\subseteq V.$

这里的 $2^V$ 实际上是代表集合 $V$ 的幂集（即所有的子集组合可能性），函数 $f$ 给每一个“选出来的元素集合”打一个分数 / 价值

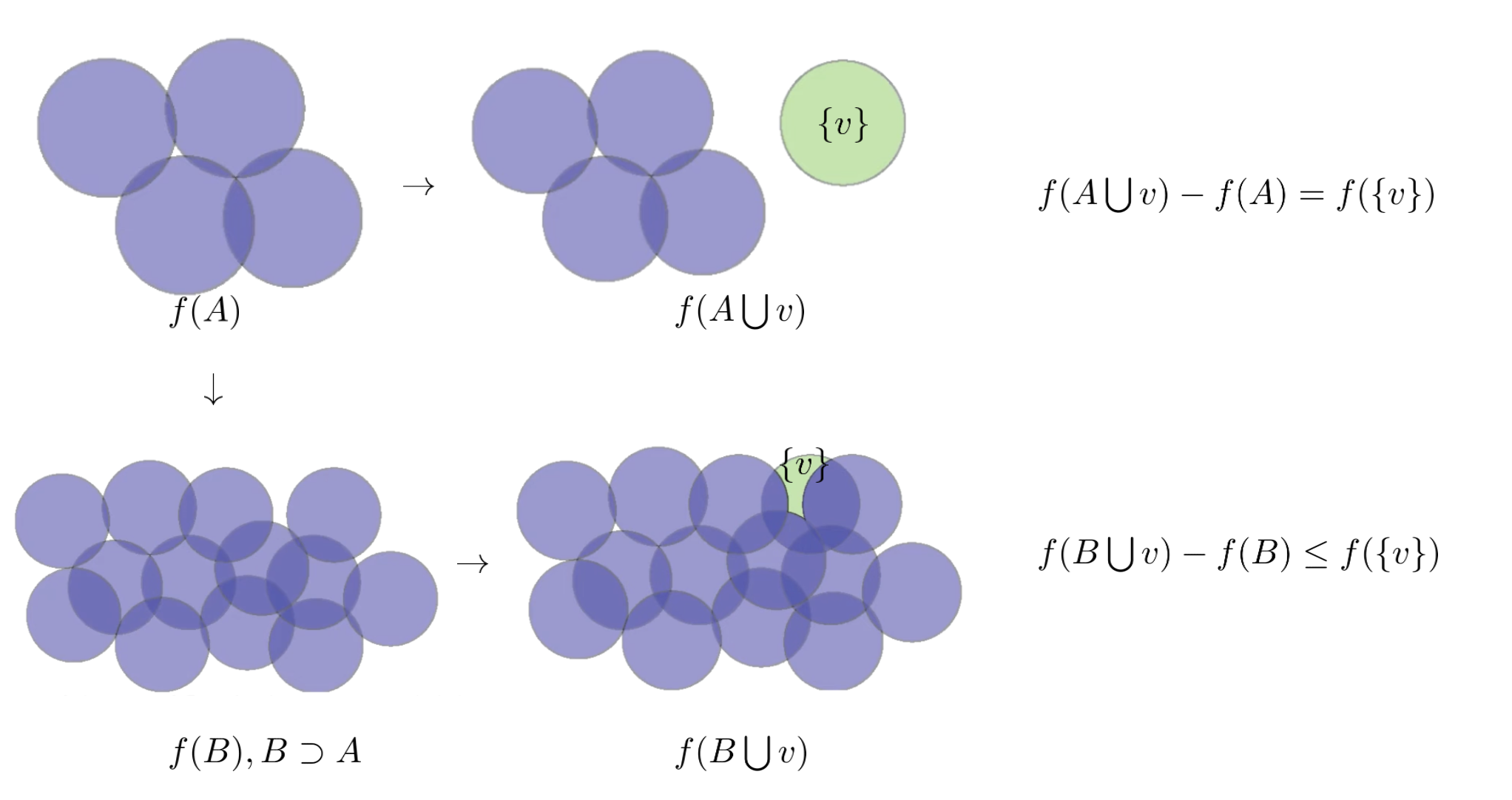
Def. 1.1.2(次模的定义，基于边际收益递减形式的（diminishing returns）): A function $f: 2^V \rightarrow \mathbb{R}$ is submodular if for any $A \subseteq B \subset V,\quad v \in V \setminus B,$ we have

$f(A \cup {v}) - f(A) \ge f(B \cup {v}) - f(B).$

即用通俗一点的说法是：同一个元素 $v$ , 在集合越大的情况下，带来的新增价值越小。

与Sub-modular对应的还有Super-modular function（超模函数）：

Def. 1.1.3(超模的定义):
$\textcircled{1}$ Given a finite ground set(有限的基集合) $V$ , a function $f: 2^V \rightarrow \mathbb{R}$ is said to be submodular if

$f(A)+f(B)\le f(A\cup B)+f(A\cap B),\quad \forall, A,B\subseteq V.$

$\textcircled{2}$ A function $f: 2^V \rightarrow \mathbb{R}$ is submodular if for any $A \subseteq B \subset V,\quad v \in V \setminus B,$ we have

$f(A \cup {v}) - f(A) \le f(B \cup {v}) - f(B).$

集合元素与向量表示：集合的特征向量/指示函数（characteristic vector and indicator function）：

Def. 1.1.4 集合的子集可以用一个特征向量表示，某元素被选中进一个子集，则表示为1，否则为0。对于一个有限集合 $V$ , 其子集 $A \subseteq V$ 可以用一个特征向量来表示： $x \in \{0,1\}^V$ , 特征向量由指示函数 $x = \mathbf{1}_A \in \{0,1\}^V$ 来定义。其中：

$\mathbf{1}_A(v) = \begin{cases} 1, & \text{if } v \in A, \\ 0, & \text{else}. \end{cases}.$

Thr 1.1.1 集合 $X$ 与特征向量 $x$ 的关系：

$x(X) \triangleq \mathbf{1}_X \quad \text{and} \quad X(x) = \{\, v \in V : x(v) = 1 \,\}.$

伪布尔函数：输入是布尔的（0/1），输出是实数（不是 0/1）的函数。因为集合与特征向量一一对应，所以集合函数也是伪布尔函数。次模函数也是伪布尔函数的一个重要的组成部分。

Def. 1.1.5 (模函数（Normalized）Modular Function) 任意一个集合函数 $m: 2^V \rightarrow \mathbb{R}$ ，对于子集 $A \subseteq V$ , 满足

$m(A) = \sum_{a \in A}m(a)$

则说明函数是Modular and Normalized。
归一化： $m(\emptyset) = 0$

模函数恰恰是子模/超模不等式在等号成立的特殊情形。

Thm 1.1.2 (模函数的性质)
$\textcircled{1}$ 可加性/线性性 (Additive/Linear)
$\textcircled{2}$ Modular functions are submodular and supermodular. 如果一个函数既是超模的又是次模的，那么这个函数就是满足模函数的。
$\textcircled{3}$ 集合的特征向量是Modular的。

集合函数的 离散优化（Discrete Optimization） 问题，即解决下列问题(在所有子集中找一个最优的)

$\min_{X \subseteq V}f(X), \quad \max_{X \subseteq V}f(X),$

如果对函数 $f$ 的结构一无所知，那么为了对某个候选解给出任何质量保证，你必须查询（评估）所有 $2^n$ 个子集。否则，得到的解可能会糟糕到没有任何下界保证。

当集合函数 $f$ 满足Submodular，那么最小化问题可以在多项式时间（Polytime）内求解；最大化问题可以得到常数因子近似解（constant-factor approximable）。

集合函数的 带约束的离散优化（Constraint Discrete Optimization） 问题，与上文的区别在于，我们只关心一些子集（不会考虑全部的子集），即考虑 $\mathcal{S} \subseteq 2^V$ . 约束的角度可以有以下几种：

规模 / 预算约束：
- 只允许 大小受限 的集合： $\mathcal{S} = { S \subseteq V : |S| \le k }$
- 某种评估指标/预算(budget)受限的集合： $\mathcal{S} = { S \subseteq V : \sum_{s \in S} w(s) \le b }$
组合结构约束：可行的集合 (S) 可能需要对应某种组合意义上可行的结构，
- 树（trees）
- 匹配（matchings）
- 路径（paths）
- 点覆盖（vertex covers）
- 割（cuts）
由另一个函数定义的约束： $\mathcal{S}$ $S$ 可能由另一个函数 $g$ $g$ 定义，例如：
- 下水平集（sub-level sets）： $\mathcal{S} = { S \subseteq V : g(S) \le \alpha }$
- 上水平集（super-level sets）： $\mathcal{S} = { S \subseteq V : g(S) \ge \alpha }$

总之，受约束的离散优化问题即求解如下问题：

$\max_{S \subseteq 2^V} f(S) \quad \text{s.t. } S \in \mathcal{S}, \quad \min_{S \subseteq 2^V} f(S) \quad \text{s.t. } S \in \mathcal{S}$

当 $f$ （以及 $g$ 是次模函数时，这些问题通常可以在具有理论保证的情况下求解，而且往往还能高效完成！

1.2 Submodularity在机器学习中有什么用？

作为物理过程的一个模型：
- 子模函数适合建模什么，取决于我们是希望最大化它，还是最小化它。
- 子模函数在建模以下方面时具有天然优势：
  - 在最大化问题中：
    多样性（diversity）、覆盖（coverage）、张成（span）、以及信息量（information）；
  - 在最小化问题中：
    协同成本（cooperative costs）、复杂度（complexity）、粗糙性（roughness）、以及不规则性（irregularity）。
子模函数可以作为机器学习策略中的一个参数：
（例如：主动学习 / 半监督学习、离散散度、用于正则化的凸范数）
子模函数本身可以作为学习对象或目标函数，
直接基于数据进行学习。
作为优化中的替代或松弛策略：
- 可作为一种不同于基于因子分解或分解化简的方法（例如在图模型中常见的那种）。

1.2.1 集合覆盖（Set Cover）与最大覆盖（Maximum Coverage）

给定一个包含 $n$ 个元素的有限集合 $V$ ，以及一个由 $m$ 个 $V$ 的子集组成的集合 $\mathcal{V} = {V_1, V_2, \ldots, V_m}$ . 其中 $V_i \subseteq V$ ，并且 $\bigcup_i V_i = V$

最小集合覆盖（Minimum Set Cover）问题：
选择一个最小的子集索引集合 $A \subseteq [m] \triangleq {1, \ldots, m}$ 使得 $\bigcup_{a \in A} V_a = V$
最大 (k) 覆盖（Maximum Coverage）问题：
给定一个整数 $k \le m$ ，选择 $k$ 个子集（例如 $\{a_1, a_2, \ldots, a_k\}$ ，其中 $a_i \in [m]$ ）, 使得 $\left| \bigcup_{i=1}^{k} V_{a_i} \right|$ 最大化。